码字总结不易，老铁们来个三连：点赞、关注、评论
作者：[左手の明天]
原创不易，转载请联系作者并注明出处
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
差分方程是描述离散时间系统的数学模型，求解差分方程是分析离散时间系统的重要内容。
目录
一阶线性常系数差分方程的平衡点及其稳定性
高阶线性常系数差分方程的平衡点及其稳定性
一阶线性常系数差分方程
濒危物种(Florida 沙丘鹤)的自然演变和人工孵化
问题提出
模型建立
模型求解
结果分析
高阶线性常系数差分方程
一年生植物的繁殖
问题提出
模型建立
模型求解
线性常系数差分方程组
汽车租赁公司的运营
问题提出
模型建立
模型求解
按年龄分组的种群增长
问题提出
模型建立
模型求解
差分方程求解方法
迭代法
时域经典法
双零法
一阶线性常系数差分方程的平衡点及其稳定性
差分方程的一般形式
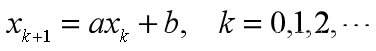
差分方程的平衡点 ~代数方程 x=ax+b 的根 x=b/(1-a)
差分方程的解
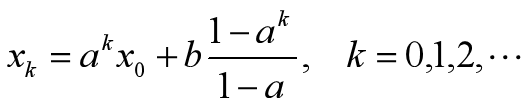
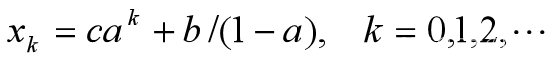
c= x0-b/(1-a)由初始值x0 和a、b确定
平衡点稳定的充要条件是 |a|<1
高阶线性常系数差分方程的平衡点及其稳定性
特征方程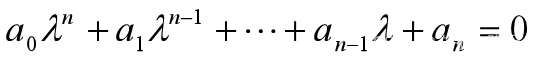 
特征根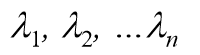
平衡点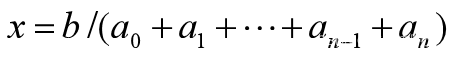
差分方程的解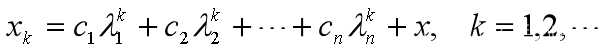
平衡点稳定的条件: 所有特征根的模小于1
一阶线性常系数差分方程
濒危物种(Florida 沙丘鹤)的自然演变和人工孵化
问题提出
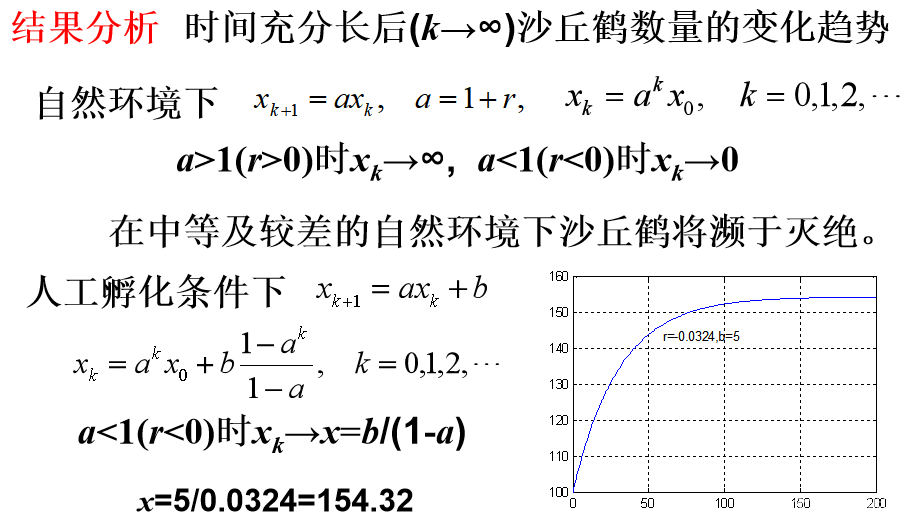
Florida沙丘鹤属于濒危物种，它在较好自然环境下，年均增长率仅为1.94%，而在中等和较差环境下年均增长率分别为 -3.24% 和 -3.82%，如果在某自然保护区内开始有100只鹤，建立描述其数量变化规律的模，并作数值计算。
如果每年人工孵化5只鹤放入该保护区， 在中等自然环境下鹤的数量将如何变化?
模型建立
记第k年沙丘鹤的数量为，年均增长率为r， 则第k+1年鹤的数量为
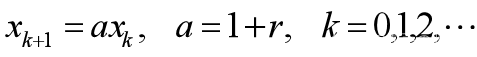
设每年人工孵化的数量为b
那么可以得到
模型求解
已知X0=100，在较好，中等和较差的自然环境下r=0.0194 , -0.0324 和 -0.0382 利用Matlab编程，递推20年后观察沙丘鹤的数量变化情况
>>X0=100;
>> r=0.0194;
>> n=20;
>>Xn=(1+r)^n*X0执行后得到： Xn =146.8563
通过函数形式实现如下：
function x=sqh(n,r)
x(1)=100;
for k=1:n
x(k+1)=(1+r)*x(k);
end
>>xn＝sqh(20,0.0194)
xn =
Columns 1 through 6
100.0000 101.9400 103.9176 105.9336 107.9888 110.0837
Columns 7 through 12
112.2194 114.3964 116.6157 118.8780 121.1843 123.5353
Columns 13 through 18
125.9318 128.3749 130.8654 133.4042 135.9922 138.6305
Columns 19 through 21
141.3199 144.0615 146.8563
利用plot 绘图观察数量变化趋势
>>k=0:20；
>>y1= sqh(20,0.0194);
>>plot(k,y1)
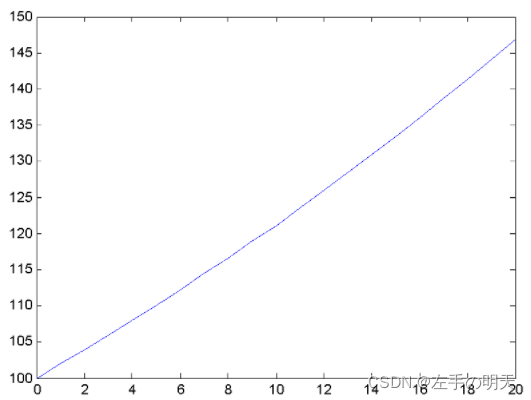
在同一坐标系下画图
>> k=0:20; %一个行向量
>> y1= sqh(20, 0.0194);
>> y2= sqh(20, -0.0324);
>> y3= sqh(20, -0.0382);
>> plot(k,y1,k,y2,':',k,y3,'r')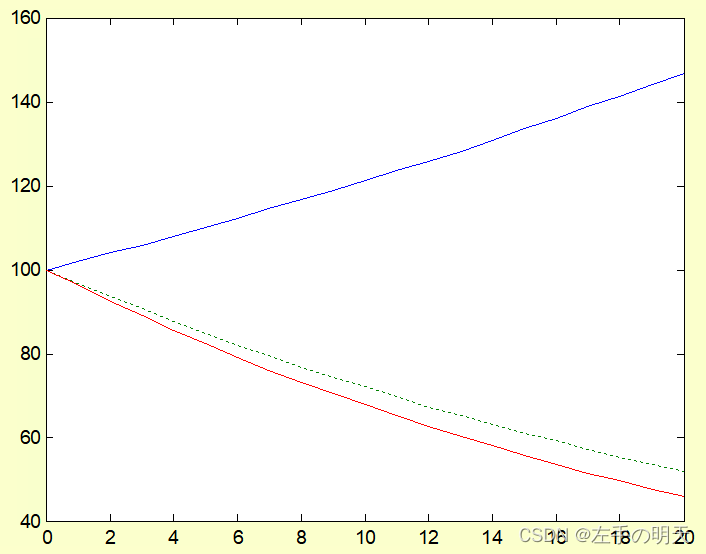
最终结果如下：
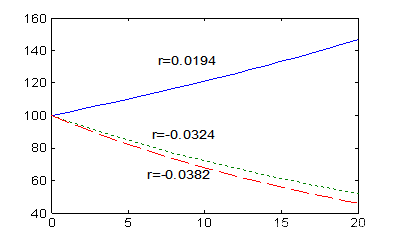
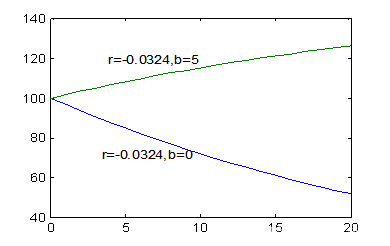
结果分析
高阶线性常系数差分方程
一年生植物的繁殖
问题提出
一年生植物春季发芽，夏天开花，秋季产种。 没有腐烂、风干、被人为掠去的那些种子可以活过冬天，其中的一部分能在第二年春季发芽，然后开花、产种，其中的另一部分虽未能发芽，但如又能活过一个冬天，则其中一部分可在第三年春季发芽，然后开花、产种，如此继续。
一年生植物只能活一年，且近似地认为，种子最多可以活过两个冬天。
建立数学模型研究植物数量的变化规律， 及它能够一直繁殖下去的条件。
模型建立
设一棵植物平均产种数为c，种子能够活过冬天的比例为b，活过冬天的那些种子在来年春季发芽的比例为，未能发芽的那些种子又活过一个冬天的比例仍为b， 在下一年春季发芽的比例为
。
~第k年的植物数量，设今年种下(并成活)的数量为
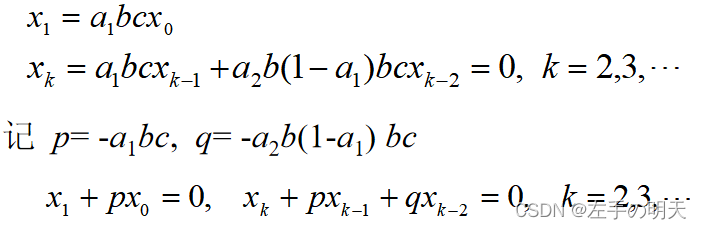
寻找形如的解
模型求解
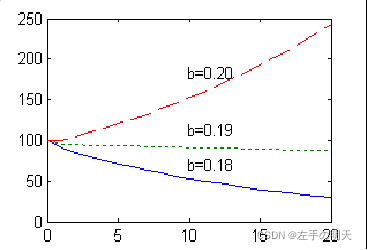
设c=10， a1=0.5，a2=0.25，b=0.18, 0.19, 0.20，x0=100
matlab建立如下函数：
function x=zwfz(x0,n,b)
c=10;a1=0.5;a2=0.25;
p=a1*b*c;q=a2*b*(1-a1)*b*c;
x(1)=x0;
x(2)=p*x(1);
for k=3:n
x(k)=p*x(k-1)+q*x(k-2);
end
>> k=0:20;
>> y1=zwfz(100,21,0.18);
>> y2=zwfz(100,21,0.19);
>> y3=zwfz(100,21,0.20);
>> plot(k,y1,k,y2,':',k,y3,'r')
差分方程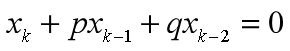
特征方程
特征根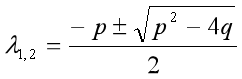 
差分方程的解
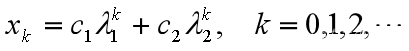常数c1, c2由x0, x1确定
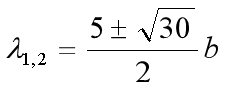
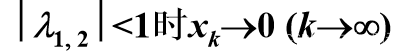
植物能够一直繁殖下去的条件为b>0.191
线性常系数差分方程组
汽车租赁公司的运营
问题提出
汽车租赁公司在3个相邻的城市运营，在一个城市租赁的汽车可以在任意一个城市归还.
- 在A市租赁在A, B, C市归还的比例分别为0.6, 0.3, 0.1
- 在B市租赁在A, B, C市归还的比例分别为0.2, 0.7, 0.1
- 在C市租赁在A, B, C市归还的比例分别为0.1, 0.3, 0.6
公司开业时将600辆汽车平均分配到3个城市， 建立运营中汽车数量在3个城市间转移的模型， 讨论时间充分长以后的变化趋势.
模型建立
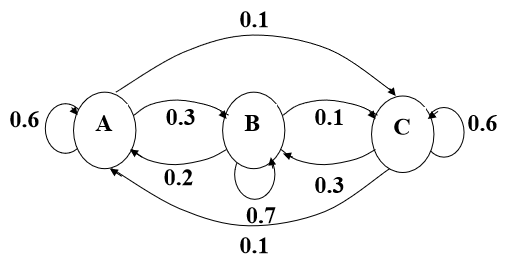
记第k个租赁期末公司在A, B, C市的汽车数量分别为x1(k),x2(k),x3(k)（也是第k+1个租赁期开始各个城市租出去的汽车数量），很容易写出第k+1个租赁期末公司在A, B, C市的汽车数量为(k=0,1,2,3···)
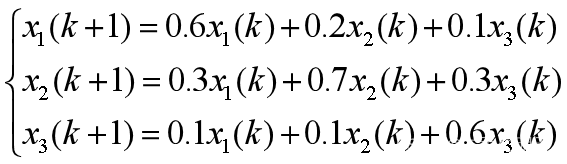
用矩阵表示
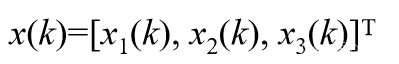
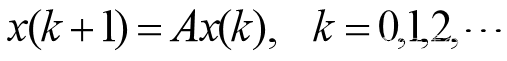
观察n年以后的3个城市的汽车数量变化情况
模型求解
>> A=[0.6,0.2,0.1;0.3,0.7,0.3;0.1,0.1,0.6];
>> n=10;
>> for k=1:n
x(:,1)=[200,200,200]';
x(:,k+1)=A*x(:,k);
end
>> x(:,k+1)
ans =
179.9324
299.9895
120.0781
时间充分长后3个城市的汽车数量趋向稳定，稳定值与初始分配无关
建立M文件
function x=qczl(n)
A=[0.6,0.2,0.1;0.3,0.7,0.3;0.1,0.1,0.6];
x(:,1)=[200,200,200]';
for k=1:n
x(:,k+1)=A*x(:,k);
end
作图观察5年以后数量的变化趋势：
>> y1=qczl(5);
>> k=0:5;
>> plot(k,y1)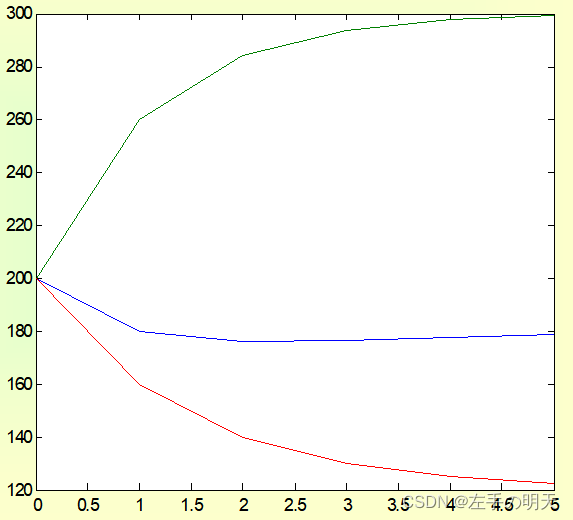
按年龄分组的种群增长
问题提出
野生或饲养的动物因繁殖而增加，因自然死亡和人为屠杀而减少，不同年龄动物的繁殖率，死亡率有较大差别，因此在研究某一种群数量的变化时，需要考虑年龄分组的种群增长。
将种群按年龄等间隔的分成若干个年龄组，时间也离散化为时段，给定各年龄组种群的繁殖率和死亡率，建立按年龄分组的种群增长模型，预测未来各年龄组的种群数量，并讨论时间充分长以后的变化趋势。
模型建立
- 种群按年龄大小等分为n个年龄组，记i=1,2,…n
- 时间离散为时段，长度与年龄组区间相等，记k=1,2,…
- 第i 年龄组1雌性个体在1时段内的繁殖率为
- 第i 年龄组在1时段内的死亡率为
，存活率为
xi(k)~时段k第i 年龄组的种群数量
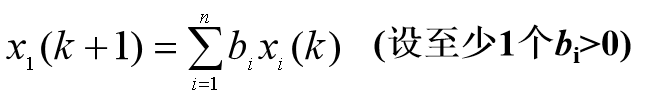
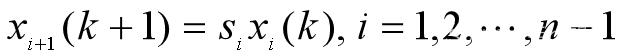
模型求解
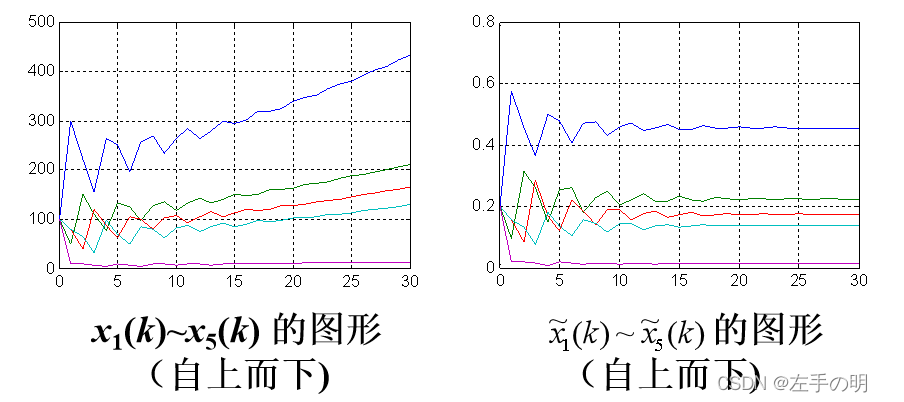
设一种群分成 n=5个年龄组，繁殖率 b1~b5= 0, 0.2, 1.8, 0.8, 0.2，存活率s1~s4= 0.5, 0.8, 0.8, 0.1，各年龄组现有数量均为100 ．
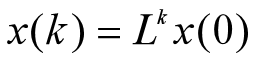
>> b=[0,0.2,1.8,0.8,0.2];
>> E=diag([0.5,0.8,0.8,0.1]);
>> L=[b;E,zeros(4,1)];
>> b=[0,0.2,1.8,0.8,0.2];
>> E=diag([0.5,0.8,0.8,0.1]);
>> L=[b;E,zeros(4,1)]; %分块矩阵
>> n=30;
>> for k=1:n
x(:,1)=[100,100,100,100,100]';
x(:,k+1)=A*x(:,k);
end
ans =
434.1877
211.4436
164.6266
128.9265
12.5635
差分方程求解方法
迭代法
差分方程本身就是一个递推方程，根据初始状态和激励信号依次迭代就可算出输出序列。迭代法是
解差分方程的基础方法, 如果所需输出序列个数较少（如计算边界条件）可手工直算，如需计算大量输出可利用计算机编程实现。
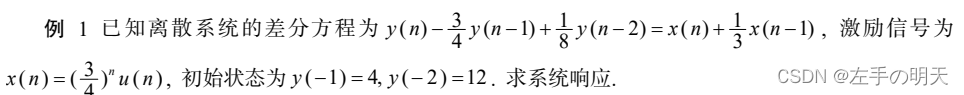
根据激励信号和初始状态，手工依次迭代可算出
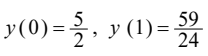
利用 MATLAB 中的 filter 函数实现迭代过程的 m 程序如下:
clc;clear;format compact;
a=[1,-3/4,1/8],b=[1,1/3,0], %输入差分方程系数向量,不足补0对齐
n=0:10;xn=(3/4).^n, %输入激励信号
zx=[0,0],zy=[4,12], %输入初始状态
zi=filtic(b,a,zy,zx),%计算等效初始条件
[yn,zf]=filter(b,a,xn,zi),%迭代计算输出和后段等效初始条件MATLAB提供的 filter函数是一个内建函数， 用 type命令看不到程序代码。为了理解迭代思想，下面根据图 所示的直接Ⅰ型结构， 重写实现迭代法的 m 程序。
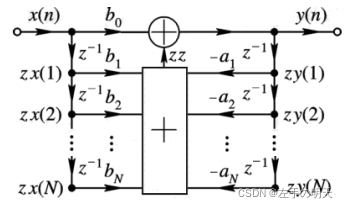
clc;clear;format compact;
a=[1, -3/4, 1/8], b=[1, 1/3, 0], %输入差分方程系数向量, 不足补 0 对齐
n=0:10;x=(3/4).^n, %输入激励信号
zx=[0, 0], zy=[4, 12], %输入初始状态
% 下面是按直接Ⅰ型结构迭代的通用程序 %
N=length(a)-1, %计算数据存储长度
L=length(x), %计算激励信号长度
y=zeros(1, L);%输出信号初始化
for i=1:L; %逐个计算输出信号
for n=1:N;z(n)=b(n+1)*zx(n)-a(n+1)*zy(n);end %分算过去
zz=sum(z);%计算输出中的过去分量
y(i)=b(1)*x(i)+zz;% 计算当前输出 y(n)
for n=N:-1:2, zx(n)=zx(n-1);zy(n)=zy(n-1);end%过去数据下移
zx(1)=x(i);zy(1)=y(i);%当前的激励和输出变为过去, 以便算下一个输出
end
%理解 filter 函数中 zf 参数的意义
zf=zeros(1, N);%初始化 zf
for k=1:N; %逐个计算 zf 参数
for n=1:N;z(n)=b(n+1)*zx(n)-a(n+1)*zy(n);end %算 z(n)
zf(k)=sum(z);% 计算第 k 个 zf
for k=N:-1:2, zx(k)=zx(k-1);zy(k)=zy(k-1);end;%过去数据下移
zx(1)=0;zy(1)=0;% 没有当前的激励和输出变为过去, 算下一个 zf
end
y, zf, %显示输出和 zf 参数时域经典法
用时域经典法求解差分方程与高等数学中求解微分方程的过程类似：先求齐次解；再将激励信号代
入方程右端化简得自由项，根据自由项形式求特解：然后根据边界条件求完全解。
用时域经典法求解例的基本步骤如下：
- (1) 求齐次解
特征方程为
，可算出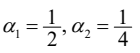
。高阶特征根可用 MATLAB 的roots 函数计算。齐次解为
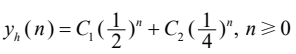
- (2) 求方程的特解
将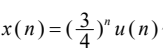
代入差分方程右端得自由项为
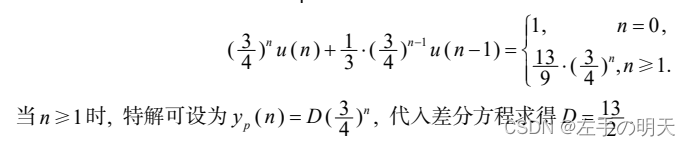
- (3) 利用边界条件求完全解
当 n = 0 时迭代求出y(0) = 5/2，当 n≥1 时 , 完全解的形式为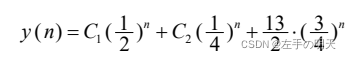
选择求完全解系数的边界条件y(0)，y(-1)。根据边界条件求得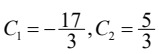
注意完全解的表达式只适于特解成立的n取值范围，其他点要用δ(n) 及其延迟表示，如果其值符合表达式则可合并处理。
差分方程的完全解为
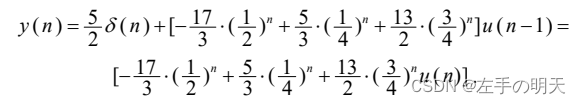
MATLAB没有专用的差分方程求解函数，但可调用maple符号运算工具箱中的rsolve函数实现，格式为
y=maple('rsolve({equs, inis},y(n))')其中
- equs为差分方程表达式
- inis为边界条件
- y(n)为差分方程中的输出函数式
在MATLAB中用时域经典法求解例1中的全响应和单位样值响应的程序如下.
clc;clear;format compact;
yn=maple('rsolve({y(n)-3/4*y(n-1)+1/8*y(n-2)=(3/4)^n+1/3*(3/4)^(n-1),y(0)=5/2,y(-1)=4},y(n))'),
hn=maple('rsolve({y(n)-3/4*y(n-1)+1/8*y(n-2)=0,y(0)=1,y(1)=13/12},y(n))'),双零法
双零法是将完全解分解成物理意义明显的零输入响应和零状态响应分别计算。
- 零输入响应是激励为零，由系统的初始状态所产生的响应；零输入响应要求差分方程右端为零，故特解为零；完全解为齐次解形式，系数可直接由初始状态确定。
- 零状态响应是初始状态为零，由激励信号所产生的响应。计算零状态响应可用时域经典法，也可用卷积法。
根据双零响应的定义，按时域经典法的求解步骤可分别求出零输入响应和零状态响应。
理解了双零法的求解原理和步骤，实际计算可调用rsolve函数实现：
yzi=maple('rsolve({y(n)-3/4*y(n-1)+1/8*y(n-2)=0,y(-1)=4, y(-2)=12},y(n))'),
yzs=maple('rsolve({y(n)-3/4*y(n-1)+1/8*y(n-2)=(3/4)^n+1/3*(3/4)^(n-1),y(0)=1, y(-1)=0},y(n))'),
