偏微分方程可以描述各种自然和工程现象， 是构建科学、工程学和其他领域的数学模型主要手段。

偏微分方程主要有三类：椭圆方程，抛物方程和双曲方程。

本文采用有限差分法求解偏微分方程，通过案例讲解一维平流方程、一维热传导方程、二维双曲方程、二维抛物方程和二维椭圆方程等常见类型的偏微分方程的数值解法，给出了全部例程和运行结果。

欢迎关注『Python小白的数学建模课 @ Youcans』系列，每周持续更新。

---

1. 偏微分方程基本知识

微分方程是指含有未知函数及其导数的关系式，偏微分方程是包含未知函数的偏导数（偏微分）的微分方程。

偏微分方程可以描述各种自然和工程现象， 是构建科学、工程学和其他领域的数学模型主要手段。 科学和工程中的大多数实际问题都归结为偏微分方程的定解问题，如：波传播，流动和扩散，振动，固体力学，电磁学和量子力学，等等。

偏微分方程主要有三类：椭圆方程，抛物方程和双曲方程。

• 双曲方程描述变量以一定速度沿某个方向传播，常用于描述振动与波动问题。
• 椭圆方程描述变量以一定深度沿所有方向传播，常用于描述静电场、引力场等稳态问题。
• 抛物方程描述变量沿下游传播，常用于描述热传导和扩散等瞬态问题。

偏微分方程的定解问题通常很难求出解析解，只能通过数值计算方法对偏微分方程的近似求解。常用偏微分方程数值解法有：有限差分方法、有限元方法、有限体方法、共轭梯度法，等等。通常先对问题的求解区域进行网格剖分，然后将定解问题离散为代数方程组，求出在离散网格点上的近似值。

Python 语言求解偏微分方程的功能是比较弱的，主要有 Fipy, FEniCS 等有限元方法的工具包，另外还有机器学习工具如 Tensorflow 也可以进行偏微分方程的仿真模拟。但是，这些工具都不适合 Python 小白学习和使用，因此本篇采用比较简单的有限差分法对 5种典型的偏微分方程进行编程，通过案例讲解偏微分方程的数值解法。

---

2. 案例一：一维线性平流方程

2.1 一维线性平流方程的数学模型

平流过程是大气运动中重要的过程。平流方程（Advection equation）描述某一物理量的平流作用而引起局地变化的物理过程，最简单的形式是一维平流方程。

{ ∂ u ∂ t + v ∂ u ∂ x = 0 u ( x , 0 ) = F ( x ) 0 ≤ t ≤ t e x a < x < x b begin{cases} begin{aligned} &frac{partial u}{partial t} + v frac{partial u}{partial x}= 0\ &u(x,0)=F(x)\ &0 leq t leq t_e\ &x_a<x<x_b end{aligned} end{cases} ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧​​∂t∂u​+v∂x∂u​=0u(x,0)=F(x)0≤t≤te​xa​<x<xb​​​

式中 u 为某物理量，v 为系统速度，x 为水平方向分量，t 为时间。

虽然该方程可以求得解析解：
u ( x , t ) = F ( x − v ∗ t ) ,   0 ≤ t ≤ t e u(x,t)=F(x-v*t), 0 leq t leq t_e u(x,t)=F(x−v∗t), 0≤t≤te​

考虑一维线性平流偏微分方程的数值解法，采用有限差分法求解。简单地， 采用一阶迎风格式的差分方法（First-order Upwind)，一阶导数的差分表达式为：
( ∂ u ∂ x ) i , j = u i + 1 , j − u i , j Δ x + O ( Δ x ) (frac{partial u}{partial x})_{i,j}=frac{u_{i+1,j}-u_{i,j}}{Delta x}+O(Delta x) (∂x∂u​)i,j​=Δxui+1,j​−ui,j​​+O(Δx)
于是得到差分方程：
u i , j + 1 = u i , j − v ∗ d t / d x ∗ ( u i , j − u i − 1 , j ) u_{i,j+1}=u_{i,j}-v*dt/dx*(u_{i,j}-u_{i-1,j}) ui,j+1​=ui,j​−v∗dt/dx∗(ui,j​−ui−1,j​)
即可递推求得该平流方程的数值解。

2.2 偏微分方程编程步骤

以该题为例一类有限差分法求解一维平流问题偏微分方程的步骤：

1. 导入numpy、matplotlib 包；
2. 定义初始条件函数 U(x,0)；
3. 输入模型参数 v, p，定义求解的时间域 (tStart, tEnd) 和空间域 (xMin, xMax)，设置差分步长 dt, nNodes；
4. 初始化；
5. 递推求解差分方程在区间 [xa,xb] 的数值解，获得网格节点的处的 u(t) 值。

在例程中，设初值条件为 F ( x ) = s i n ( 2 ∗ ( x − p ) 2 ) F(x) = sin(2 * (x-p)^2) F(x)=sin(2∗(x−p)2)，取 $v=1.0,p=0.25$，空间域 $x\in (0,\pi )$。

2.3 Python 例程：偏微分方程（一维平流方程）

# mathmodel13_v1.py
# Demo10 of mathematical modeling algorithm
# Solving partial differential equations
# 偏微分方程数值解法

import numpy as np
import matplotlib.pyplot as plt

# 1. 一维平流方程 (advection equation)
# U_t + v*U_x = 0

# 初始条件函数 U(x,0)
def funcUx0(x, p): 
    u0 = np.sin(2 * (x-p)**2)
    return u0

# 输入参数
v1 = 1.0  # 平流方程参数，系统速度
p = 0.25  # 初始条件函数 u(x,0) 中的参数

tc = 0  # 开始时间
te = 1.0  # 终止时间: (0, te)
xa = 0.0  # 空间范围: (xa, xb)
xb = np.pi
dt = 0.02  # 时间差分步长
nNodes = 100  # 空间网格数

# 初始化
nsteps = round(te/dt)
dx = (xb - xa) / nNodes
x = np.arange(xa-dx, xb+2*dx, dx)
ux0 = funcUx0(x, p)

u = ux0.copy()  # u(j)
ujp = ux0.copy()  # u(j+1)

# 时域差分
for i in range(nsteps):
    plt.clf()  # 清除当前 figure 的所有axes, 但是保留当前窗口

    # 计算 u(j+1)
    for j in range(nNodes + 2):
        ujp[j] = u[j] - (v1 * dt/dx) * (u[j] - u[j-1])

    # 更新边界条件
    u = ujp.copy()
    u[0] = u[nNodes + 1]
    u[nNodes+2] = u[1]

    # 绘图
    plt.plot(x, u, 'b-', label="v1= 1.0")
    plt.axis((xa-0.1, xb + 0.1, -1.1, 1.1))
    plt.xlabel("x")
    plt.ylabel("U(x)")
    plt.legend(loc=(0.05,0.05))
    plt.title("Advection equation with finite difference method, t = %1.f" % (tc + dt))
    plt.text(0.05,0.9,"youcans-xupt",color='gainsboro')
    plt.pause(0.001)
    tc += dt

plt.show()

2.4 Python 例程运行结果

---

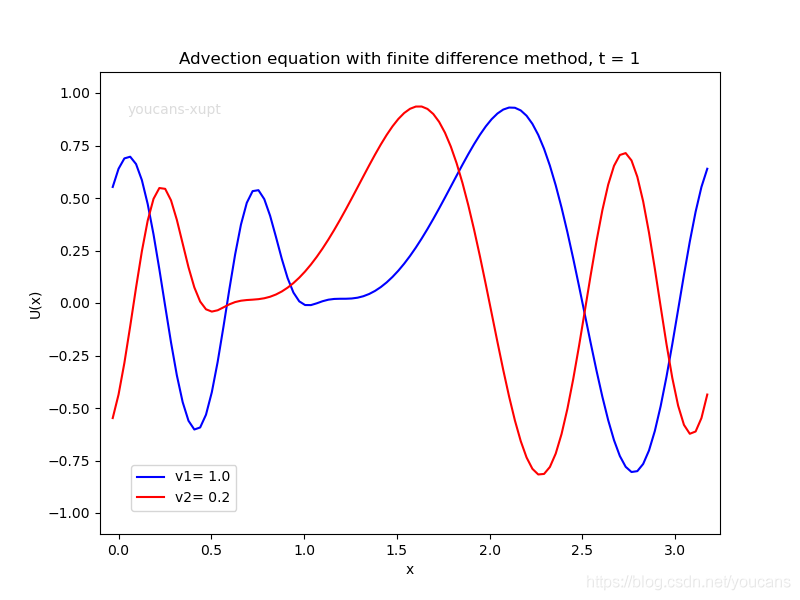
3. 案例二：一维热传导方程

3.1 一维热传导方程的数学模型

热传导方程描述一个区域内的温度随时间的变化，是典型的抛物型偏微分方程，也称为扩散方程。

一维热传导方程考虑各向同性的均匀细杆，在垂直于 x 轴的截面上的温度相同，细杆的圆周与周围环境无热交换，杆内无热源，则温度 $u=u(t,x)$ 是时间变量 t 和水平方向空间变量 x 的函数。

{ ∂ u ∂ t = d i v ( U u ) = λ ∂ 2 u ∂ x 2 u ( x , 0 ) = u 0 ( x ) u ( x a ) = u a ( t ) ,   u ( x b , t ) = u b ( t ) 0 ≤ t ≤ t e ,   x a < x < x b begin{cases} begin{aligned} &frac{partial u}{partial t} = div(U_u) = lambda frac{partial ^2u}{partial x^2}\ &u(x,0)=u_0(x)\ &u(x_a)=u_a(t), u(x_b,t)=u_b(t)\ &0leq t leq t_e, x_a < x < x_b end{aligned} end{cases} ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧​​∂t∂u​=div(Uu​)=λ∂x2∂2u​u(x,0)=