一.Malthus模型（指数模型）

（1）提出以及假设

指数增长模型，由马尔萨斯在1798年提出

基本假设：人口（相对）增长率r是常数（r很小）
相对增长率 = 出生率 － 死亡率

（2）影响人口增长的因素

人口的基数
出生率和死亡率
年龄结构
性别比例
工农业生产水平
医疗水平
政府出台的政策
民族政策
…

（3）建立模型

我们用 x(t) 表示 t 时刻的人口

那么有 $$x(t+△t)-x(t)=rx(t)△t$$ (其中x为人口基数)

所以 ( x ( t + △ t ) − x ( t ) ) △ t = r x ( t ) frac{(x(t+△t) - x(t)) }{ △t} = rx(t) △t(x(t+△t)−x(t))​=rx(t)

根据高数知识，求得 d x d t = r x , x ( 0 ) = x 0 frac{dx }{dt} = rx, x(0) = x_{0} dtdx​=rx,x(0)=x0​

求得： x ( t ) = x 0 e r t x(t) = x_{0}e^{rt} x(t)=x0​ert

结论：随着时间的增加，人口按指数规律无限增长

（4）结论

可以进行短期的人口预测，较为符合
但是之后误差就很大了

（5）举例（Matlab代码）

eg：已知一组数据如下：

t = [1790 1800 1810 1820 1830 1840 1850 1860 1870 1880 1890 1900];
p = [3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0];
t为年份，p为对应的人口数量，单位为：百万

因为马尔萨斯模型为指数函数为了线性拟合数据，我们对其进行如下操作：

两边同时取对数：

可得： l n ( x ) = l n ( x 0 ) + r t ln(x) = ln(x_{0}) + rt ln(x)=ln(x0​)+rt

t = [1790 1800 1810 1820 1830 1840 1850 1860 1870 1880 1890 1900];
p = [3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0];
y = log(p);  %求ln(p)函数值
a = polyfit(t,y,1)  %用一次多项式对t和y进行拟合
z = polyval(a,t);  %求得以a为系数的多项式在t处的函数值
z1 = exp(z)
r = a(1)
plot(t,p,'bo',t,z1,'r')  %分别画出散点图以及拟合曲线图
xlabel('时间');
ylabel('人口数量');
legend('实际数据','理论曲线');

作图如下（短期内基本吻合）：

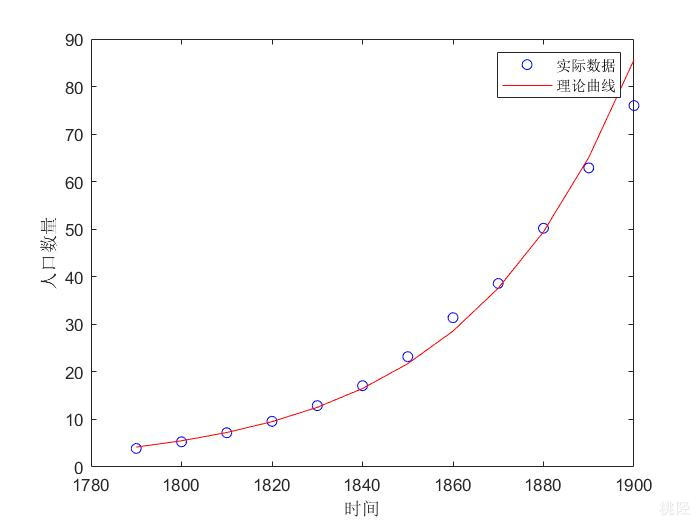
输出结果如下：

%结果如下，增长率r=0.0274
a =

    0.0274  -47.6717


z1 =

  列 1 至 5

    4.1884    5.5105    7.2498    9.5382   12.5488

  列 6 至 10

   16.5097   21.7209   28.5769   37.5969   49.4640

  列 11 至 12

   65.0769   85.6179


r =

    0.0274

$当我们用更多的数据进行长期拟合是就会发现该方法做出来的差别较大！$

---

二.Logistic模型（阻滞增长模型）

（1）背景

由于人口不可能无限制的增长，当人口达到一定数量后，那么增长率就会下降。
我们要模拟这种增长率的变化
这里简化的将增长率 r 看做是人口 x 的减函数

（2）建立 r 的关系式

假设$r(x)=r-sx(r,s>0)$ 当x很小时，r仍为固有增长率，s为待求系数

x_m 是当前环境可以容纳的最大人口容量

r ( x m ) = 0 − − > s = r x m − − > r ( x ) = r ( 1 − x x m ) r(x_{m}) = 0 --> s = frac{r }{ x_{m}} --> r(x) = r(1-frac{x}{x_{m}}) r(xm​)=0−−>s=xm​r​−−>r(x)=r(1−xm​x​)

（3）模型建立

指数增长模型： d x d t = r x frac{dx }{ dt} = rx dtdx​=rx

所以 d x d t = r ( x ) x = r x ( 1 − x x m ) frac{dx }{ dt} = r(x)x = rx(1-frac{x}{x_{m}}) dtdx​=r(x)x=rx(1−xm​x​)

最终得到： x ( t ) = x m ( 1 + ( x m x 0 − 1 ) e − r t ) x(t) =frac{x_{m}} {(1+(frac{x_{m}}{x_{0}} - 1) e^{-rt})} x(t)=(1+(x0​xm​​−1)e−rt)xm​​

（4）结论

最终得到 s 型增长曲线，x增长先快后慢，最终接近峰值 x_m

该模型同样可以用于种群数量中（鱼群的捕捞要控制在 x_m/2 附近，而害虫的防治要远远低于 x_m / 2）

（5）举例（Matlab代码）

已知一组数据同上：
t = [1790 1800 1810 1820 1830 1840 1850 1860 1870 1880 1890 1900];
p = [3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0];
t为年份，p为对应的人口数量，单位为：百万

我 们 使 用 非 线 性 拟 合 法 来 计 算 参 数 r 以 及 x m {color{Red}我们使用非线性拟合法来计算参数 r 以及 x_{m}} 我们使用非线性拟合法来计算参数r以及xm​

下面代码由两个文件构成：

$\bullet$ 主函数文件（脚本文件）

%代码如下
t = [1790 1800 1810 1820 1830 1840 1850 1860 1870 1880 1890 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990];
p = [3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 251.4];
t = t-1780; %整体减去1780
x0 = [150,0.15]; %待定参数x的初值（自己根据实际情况给出初值，之后再不断调整；其中第一个参数为最大人口数，第二个参数为人口增长率）
x = lsqcurvefit('population',x0,t,p) %使用函数求得最终的（xm，r）
p1 = population(x,t);
plot(t+1780,p,'o',t+1780,p1,'-r*')
title('Logistic模型拟合图')
xlabel('年');
ylabel('人口数');
legend('实际数据','理论数据')

$\bullet$ 函数m文件(注意文件名称与函数名称相同)

%population.m函数文件
function g = population(x,t)
%UNTITLED2 此处显示有关此函数的摘要
%   此处显示详细说明
g = x(1)./(1+(x(1)/3.9-1)*exp(-x(2)*t));  %这里的公式代入的是3.9，也就是初始数据，根据自己的初值进行修改
end

如图所示两个文件：

---

$作图如下：$

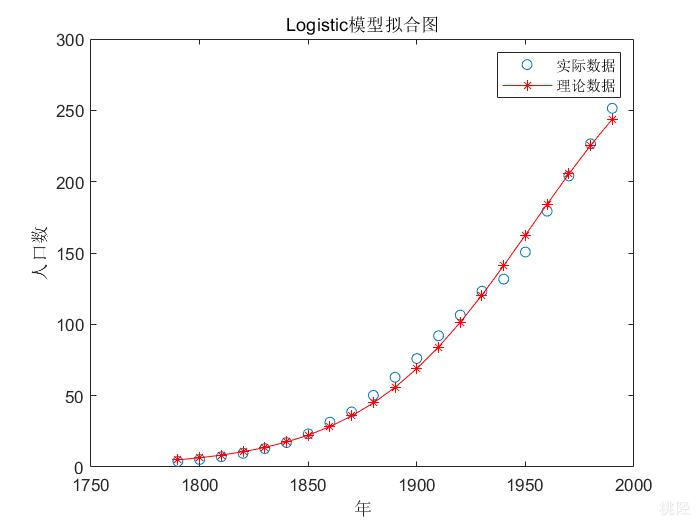
$结果如下：$

%第一个参数为 Xm，第二个参数为 r
x =

  337.4308    0.0257

三.总结

Malthus 和 Logistic 均为宏观模型，它们考虑的方面比较少。而且不考虑年龄分布。

以下的微观模型考虑年龄结构
$\bullet$ Leslie差分方程模型
$\bullet$ Verhulst偏微分方程模型
$\bullet$ Pollard随机方程模型